Use Er Diagram To Represent The Data Modeling

Chapter 6. Entity-Relationship Modelling

Table of contents

• Objectives
• Introduction
• Context
• Entities, attributes and values
  • Entities
  • Attributes
  • Values
  • Primary key data elements
  • Key
  • Candidate keys
  • Foreign keys
• Entity-Relationship Modelling
  • Entity representation
  • One-to-one relationships between two entities
  • One-to-many relationships between two entities
  • Many-to-many relationships between two entities
  • Recursive relationships
• Relationship participation condition (membership class)
  • Mandatory and optional relationships
  • One-to-one relationships and participation conditions
    • Both ends mandatory
    • One end mandatory, other end optional:
    • One end optional, other end mandatory:
    • Both ends optional:
  • One-to-many relationships and participation conditions
    • Both ends mandatory:
    • One end mandatory, other end optional:
    • One end optional, other end mandatory:
    • Both ends optional:
  • Many-to-many relationships and participation conditions
    • Both ends mandatory:
    • One end mandatory, other end optional:
    • One end optional, other end mandatory:
    • Both ends optional
• Weak and strong entities
• Problems with entity-relationship (ER) models
  • Fan traps
  • Chasm traps
• Converting entity relationships into relations
  • Converting one-to-one relationships into relations
    • Mandatory for both entities
    • Mandatory for one entity, optional for the other entity
    • Optional for both entities
  • Converting one-to-many relationships into relations
    • Mandatory for both entities
    • Mandatory for one entity, optional for another entity: many end mandatory
    • Mandatory for one entity, optional for another entity: many end optional
    • Optional for both entities
  • Converting many-to-many relationships into relations
    • Mandatory for both entities
    • Mandatory for one entity, optional for the other entity
    • Optional for both entities
  • Summary of conversion rules
• Review questions

Objectives

At the end of this chapter you should be able to:

• Analyse a given situation to identify the entities involved.

• Be able to identify the relationships between entities, and carry out any necessary transformations.

• Develop the model further by identifying attributes for each entity.

• Map the entities into tables suitable for Relational database implementation.

Introduction

In parallel with this chapter, you should read Chapter 11 of Thomas Connolly and Carolyn Begg, "Database Systems A Practical Approach to Design, Implementation, and Management", (5th edn.).

This chapter is the first to address in detail the extremely important topic of database design. The main approach described in this chapter is called Entity-Relationship Modelling. This technique has become a widely used approach in the development of database applications. The approach is essentially top-down, in that the first step is to look overall at the requirements for the application being developed, identifying the entities involved. The approach progresses from that point through the development of a detailed model of the entities, their attributes and relationships. The Entity-Relationship Modelling process is not formal, in the mathematical sense, but to be done well, it requires a consistent precision to be applied to the way that entities, their relationships and their attributes are discussed. The approach can be supplemented by methods which are more formal in their approach, and that provide a bottom-up perspective to the design process. The most commonly used of these approaches is Normalisation, which will be a core topic of the later chapters on database design.

Context

This chapter introduces the ideas of top-down database design, and provides the starting point in learning how to develop a database application. The chapter links closely with the others covering database design (Normalisation and other design topics). The chapter also has considerable relevance for the material in the module on performance tuning, such as the chapter on indexing, as the decisions made during database design have a major impact on the performance of the application.

Entities, attributes and values

Entities

Many organisations (such as businesses, government departments, supermarkets, universities and hospitals) have a number of branches, divisions or sections in order to deal with a variety of functions or different geographical areas. Each branch, division or section may itself be split up into smaller units. It is possible to regard each branch, division or section (or each unit within these) as an organisation in its own right. Organisations require information in order to carry out the tasks and activities for which they are responsible. The information that these organisations need could be categorised in a number of ways, for example:

People

• Payroll

• Pensions

• Annual leave

• Sick leave

Things

• Furniture

• Equipment

• Stationery

• Fire extinguishers

Locations

• Offices

• Warehouses

• Stock rooms

Events

• Sale is made

• Purchase order is raised

• Item is hired

• Invoice is issued

Concepts

• Image of product

• Advertising

• Marketing

• Research and development.

Each of these can be regarded as an entity.

Important

Entity

An entity may represent a category of people, things, events, locations or concepts within the area under consideration. An entity instance is a specific example of an entity. For example, John Smith is an entity instance of an employee entity.

Attributes

Entities have attributes. The following are typical of the attributes that an entity might possess:

Entity: House

Attributes:

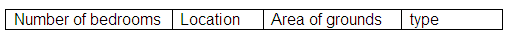
Entity: Book

Attributes:

Entity: Employee

Attributes:

Important

Attribute

An entity may have one or more attributes associated with it. These attributes represent certain characteristics of the entity; for a person, attributes might be name, age, address, etc.

Values

Using the entities and attributes shown above, the following are examples of one set of values for a particular instance of each entity. Every occurrence of an entity will have its own set of values for attributes it possesses.

Entity: House

Attributes:

Values:

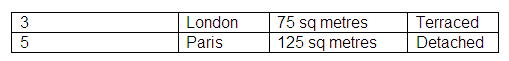
Entity: Book

Attributes:

Values:

Entity: Employee

Attributes:

Values:

Primary key data elements

If the value of certain attributes (or perhaps just one attribute) is known for a particular entity, this enables us to discover the value of other attributes associated with that entity. The attributes (or attribute) which possess this quality are known as keys, because they are able to 'unlock' the values of the other attributes that are associated with that specific instance of an entity. Why do we need a key? Suppose we had two members of staff with the same (or similar) names, such as Linda Clark and Lydia Clark. It would be a simple mistake to record something in the file of Linda Clark that should be kept in the file for Lydia Clark (or the other way around). It would be even more difficult to tell them apart if the name was given as just an initial and surname.

Some names may be spelt slightly differently, but sound similar (such as Clark and Clarke), and therefore pose a further risk of identifying the wrong member of staff.

Key

The addition of a staff number as the primary key would enable us to be sure that when we needed to refer to one or other of these members of staff, we had identified the correct individual. In this way 11057 Clark can be distinguished from 28076 Clark.

The following are examples of key data elements:

• The payroll number (primary key) of a member of staff enables us to find out the name, job title and address for that individual.

• The account number (primary key) enables us to find out whether the balance of that account is overdrawn.

• The item code (primary key) in a stationery catalogue enables us to order a particular item in a particular size and colour (e.g. a red A4 folder).

Sometimes we may need to use more than one attribute in order to arrive at a key that will provide unique identification for all the other data elements. When considering which attribute (or combination of attributes) might be used as a primary key, these attributes are known as candidate keys.

Candidate keys

Where there is more than one set of attributes which could be chosen as the primary key for an entity, each of these groups of attributes are known as candidate keys.

A company might choose either an employee's staff number or an employee's National Insurance number as the primary key, as each will provide unique identification of an individual. (Note that in different countries, a slightly different term might be used for a national code that is used to identify any one individual, such as national ID number, etc.) The staff number and the National Insurance number are candidate keys, until one is selected as the primary key.

At times we may refer to a collection of attributes that includes the primary key (for example, staff number and staff name); this group of attributes is sometimes known as a superkey.

When we need to connect together different items of data (for example, customers and items, in order to produce orders and invoices), we can do this by including the primary key of one entity as a data item in another entity; for example, we would include the primary key of Customer in the Order entity to link customers to the Orders they have placed.

Foreign keys

When a copy of the primary key for one entity is included in the collection of attributes of another entity, the copy of the primary key held in the second entity is known as a foreign key.

A foreign key enables a link to be made between different entities.

Entity-Relationship Modelling

Entity representation

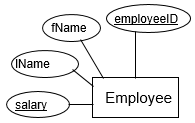
One common method to represent an entity is to use entity-relationship diagrams, where each entity is represented by a box with two compartments, the first for entity name and the second for attributes.

You may also come across diagrams that employ ellipses to represent the attributes belonging to each entity.

The relationships that exist between two entities can be categorised according to the following:

• one-to-one

• one-to-many

• many-to-many

In some cases, for simplicity, the attributes are omitted in the entity diagram.

One-to-one relationships between two entities

In a concert hall, each ticket holder has a seat for a single performance (the seat number will appear on the ticket). Only one person can sit in one seat at each performance; the relationship between a member of the audience and a seat is therefore one-to-one.

Each seat in the concert hall can be sold to one person only for a particular performance; the relationship between the seat and the member of the audience with a ticket for that seat is also one-to-one.

Relationships between entities and attributes, between attributes, and between entities can be shown in a variety of diagrammatic formats. The common format is to represent each relationship as a line. The style of the line shows the type of relationship being represented. Here, in order to represent a one-to-one relationship, a single straight line is used between the two entities.

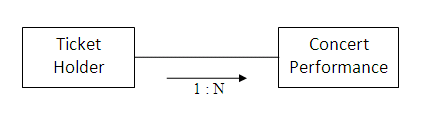
The overall relationship between ticket holders and seats is one-to-one for each performance. The entity-relationship diagram above shows the one-to-one link between a ticket holder and a concert hall seat.

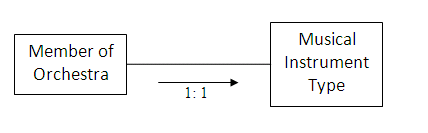
In an orchestra, each individual will play one type of musical instrument; for example, a person who plays a violin will not play a trumpet. The relationship is one-to-one from a member of the orchestra to a type of instrument.

One-to-many relationships between two entities

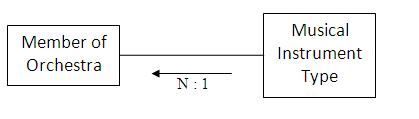
An orchestra will have more than one musician playing a particular type of instrument; for example, it is likely that there will be several members of the orchestra each playing a violin. The relationship is therefore one-to-many from a type of musical instrument to a member of the orchestra.

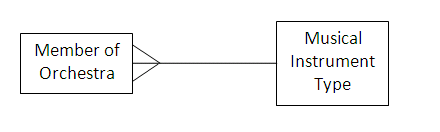
The entity-relationship diagram shows that there is a one-to-many relationship between musical instrument types and members of the orchestra. The 'crow's foot' link shows that there may be more than one member of the orchestra for each type of musical instrument.

Many-to-many relationships between two entities

An individual may attend a series of concerts during each season as a member of the audience; the relationship between an individual and the concerts is one-to-many.

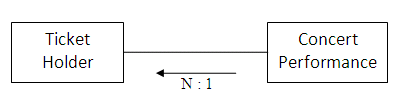
Many ticket holders will attend each concert; the relationship between a concert and members of the audience is also one-to-many.

As the relationship is one-to-many on both sides of the relationship, the relationship that exists between the two entities can be described as many-to-many.

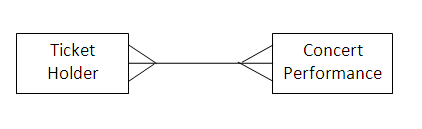
The entity-relationship diagram above has a 'crow's foot' connection at each end, illustrating that there is a many-to-many relationship between ticket holders and concert performances, as one ticket holder may attend many performances, and each performance is likely to have many ticket holders present.

As it is difficult to implement a many-to-many relationship in a database system, we may need to decompose a many-to-many relationship into two (or more) one-to-many relationships. Here, we might say that there is a one-to-many relationship between a ticket holder and a ticket (each ticket holder may have several tickets, but each ticket will be held by only one person).

We could also identify a one-to-many relationship between a concert performance and a ticket (each ticket for a particular seat will be for only one performance, but there will be many performances each with a ticket for that seat).

This allows us to represent the many-to-many relationship between ticket holder and concert performance: two one-to-many relationships involving a new entity called Ticket For Seat. This new structure can then be implemented within a Relational database system.

Recursive relationships

The relationships we have seen so far have all been between two entities; this does not have to be the case. It is possible for an entity to have a relationship with itself; for example, an entity Staff could have a relationship with itself, as one member of staff could supervise other staff. This is known as a recursive or involute relationship, and would be represented in an entity-relationship diagram as shown below.

Exercises

Exercise 1: Identifying entities and attributes

Benchmarque International, a furniture company, keeps details Of items it supplies to homes and offices (tables, chairs, bookshelves, etc). What do you think would be the entities and attributes the furniture company would need to represent these items?

Exercise 2: Identification of primary keys

What do you think would make a suitable primary key for the entity (or entities) representing the tables, chairs, bookshelves and other items of furniture for Benchmarque International?

In other words, what are the candidate keys?

Exercise 3: Identifying relationships

At a conference, each delegate is given a bound copy of the proceedings, containing a copy of all the papers being presented at the conference and biographical details of the speakers.

What is the relationship between a delegate and a copy of the proceedings?

Draw the entity-relationship diagram.

Exercise 4: Identifying relationships II

Many papers may be presented at a conference.

Each paper will be presented once only by one individual (even if there are multiple authors).

Many delegates may attend the presentation of a paper.

Papers may be grouped into sessions (two sessions in the morning and three in the afternoon).

What do you think is the relationship between:

• a speaker and a paper

• a paper and a session

Exercise 5 — Identifying relationships III

A conference session will be attended by a number of delegates. Each delegate may choose a number of sessions. What is the relationship between conference delegates and sessions? Draw the entity-relationship diagram.

Relationship participation condition (membership class)

Mandatory and optional relationships

We can extend the entity-relationship model by declaring that some relationships are mandatory, whereas others are optional. In a mandatory relationship, every instance of one entity must participate in a relationship with another entity. In an optional relationship, any instance of one entity might participate in a relationship with another entity, but this is not compulsory.

Important

Participation condition/membership class

The participation condition defines whether it is mandatory or optional for an entity to participate in a relationship. This is also known as the membership class of a relationship.

As there are two kinds of participation conditions (mandatory and optional), and most entities are involved in binary relationships, it follows that there are four main types of membership relationships, as follows:

1. Mandatory for both entities

2. Mandatory for one entity, optional for the other

3. Optional for one entity, mandatory for the other

4. Optional for both entities

It might be tempting to think that options 2 and 3 are the same, but it is important to recognise the difference, particularly when thinking about whether the relationship is one-to-one, one-to-many or many-to-many. A useful analogy is to think of a bank, with customers who have savings accounts and loans. It may be the bank's policy that any customer must have a savings account before they are eligible to receive a loan, but not all customers who have savings accounts will require a loan.

We can examine how these different types of membership classes can be used to reflect the policies of allocating staff within departments. We would expect any member of staff in an organisation to work in a given department, but what happens if a new department is created, or a new member of staff joins? If we look at each combination in turn, we can see what the possibilities are:

1. Mandatory for both entities: A member of staff must be assigned to a given department, and any department must have staff. There can be no unassigned staff, and it is not possible to have an 'empty' department.

2. Mandatory for one entity, optional for the other: Any member of staff must be attached to a department, but it is possible for a department to have no staff allocated.

3. Optional for one entity, mandatory for the other: A member of staff does not have to be placed in a department, but all departments must have at least one member of staff.

4. Optional for both entities: A member of staff might be assigned to work in a department, but this is not compulsory. A department might, or might not, have staff allocated to work within it.

We can elaborate the standard entity-relationship notation with a solid circle to indicate a mandatory entity, and a hollow circle for an optional entity (think of the hollow circle like 'o' for optional). (You may find alternative notations in other texts - for example, a solid line to represent a mandatory entity, and a dotted line to indicate an optional entity. Another method places solid circles inside entity boxes for mandatory participation, or outside entity boxes for optional membership.) The use of a graphical technique enables us to represent the membership class or participation condition of an entity and a relationship in an entity-relationship diagram.

We will now explore these possibilities using a performer, agents and bookings scenario as an example, but experimenting with different rules to see what effect they have on the design of the database. Supposing to start with, we have the following situation.

There are a number of performers who are booked by agents to appear at different venues. Performers are paid a fee for each booking, and agents earn commission on the fee paid to each performer. We will now consider relationships of different kinds between these entities.

One-to-one relationships and participation conditions

Both ends mandatory

It might be the case that each performer has only one agent, and that all bookings for any one performer must be made by one agent, and that agent may only make bookings for that one performer. The relationship is one-to-one, and both entities must participate in the relationship.

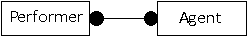
The solid circle at each end of the relationship shows that the relationship is mandatory in both directions; each performer must have an agent, and each agent must deal with one performer.

One end mandatory, other end optional:

It might be possible for agents to make bookings that do not involve performers; for example, a venue might be booked for an art exhibition. Each performer, however, must have an agent, although an agent does not have to make a booking on behalf of a performer.

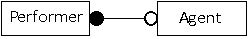
The solid circle at the performer end of the relationship illustrates that a performer must be associated with an agent. The hollow circle at the agent end of the relationship shows that an agent could be associated with a performer, but that this is not compulsory. Each performer must have an agent, but not all agents represent performers.

One end optional, other end mandatory:

It might be possible for performers to make bookings themselves, without using an agent. In this case, one performer might have an agent, and that agent will make bookings for that performer. On the other hand, a different performer might elect to make their own bookings, and will not be represented by an agent. All agents must represent a performer, but not all performers will be represented by agents. The relationship is optional for the performer, but mandatory for the agent, as shown in the diagram below.

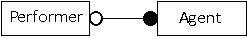
The solid circle at the agent end of the relationship shows each agent must be associated with a performer. The hollow circle at the performer end of the relationship indicates that a performer could be represented by an agent, but that this is not compulsory. Each agent must deal with only one performer, but each performer does not have to have an agent.

Both ends optional:

Another possibility is that agents may make bookings that do not involve performers; for example, a venue might be booked for an art exhibition. In addition, performers may make bookings themselves, or might have bookings made by an agent, but if a performer has an agent, there must be a one-to-one relationship between them. This relationship is optional for both entities.

The hollow circles show that there is an optional relationship between a performer and an agent; if there is a relationship, it will be one-to-one, but it is not compulsory either for the performer or for the agent.

One-to-many relationships and participation conditions

It might be the case that a performer has only one agent, and that all bookings for any one performer must be made by one agent, although any agent may make bookings for more than one performer.

Both ends mandatory:

A performer must have one or more bookings; each booking must involve one performer.

The membership class is mandatory for both entities, as shown by the solid circle. In this case, it is not possible for a booking to be made for an event that does not involve a performer (for example, a booking could not be for an exhibition).

One end mandatory, other end optional:

A performer must have one or more bookings, but a booking might not involve a performer (e.g. a booking might be for an exhibition, not a performer).

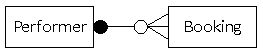
The solid circle shows the compulsory nature of the relationship for a performer; all performers must have bookings. The hollow circle shows that it is optional for a booking to involve a performer. This means that a performer must have a booking, but that a booking need not have a performer.

One end optional, other end mandatory:

A performer might have one or more bookings; each booking must involve one performer.

The membership class is mandatory for a booking, but optional for a performer. This means that it would not be possible for a booking to be for an exhibition, as all bookings must involve a performer. On the other hand, it is not compulsory for a performer to have a booking.

Both ends optional:

A performer might have one or more bookings; a booking might be associated with a performer.

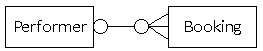
In this case, a booking could be for an exhibition as it is optional for a booking to involve a performer, as indicated by the hollow circle. A performer might decline to accept any bookings; this is acceptable, as it is optional for a performer to have a booking (shown by the hollow circle).

Many-to-many relationships and participation conditions

We could say that there is a many-to-many relationship between performers and agents, with each agent making bookings for many performers, and each performer having bookings made by many agents. We know that we need to decompose many-to-many relationships into (usually) two one-to-many relationships, but we can still consider what these many-to-many relationships would look like before this decomposition has taken place. We will see later that many-to-many relationships can be converted into relations either after they have been decomposed, or directly from the many-to-many relationship. The result of the conversion into relations will be the same in either case.

Both ends mandatory:

An example here might be where each performer must be represented by one or more agents, and each agent is required to make bookings for a number of performers.

There is a many-to-many relationship between the two entities, in which both entities must participate. Agents are not allowed to make bookings for events that do not involve performers (such as conferences or exhibitions). Performers must have bookings made by agents, and are not allowed to make their own bookings.

One end mandatory, other end optional:

In this example, it is still necessary for performers to be represented by a number of agents, but the agents now have more flexibility as they do not have to make bookings for performers.

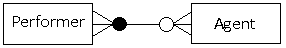
There is a many-to-many relationship between the two entities; one must participate, but it is optional for the other entity.

One end optional, other end mandatory:

Here, performers have the flexibility to make their own bookings, or to have bookings made by one or more agents. Agents are required to make bookings for performers, and may not make arrangements for any other kind of event.

There is a many-to-many relationship between the two entities; it is optional for one to participate, but participation is mandatory for the other entity.

Both ends optional

Here, performers and agents are both allowed a degree of flexibility. Performers may make their own bookings, or may have agents make bookings for them. Agents are permitted to make bookings for a number of performers, and also have the ability to make other kinds of bookings where performers are not required.

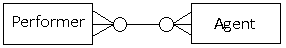
There is a many-to-many relationship between the two entities; participation is optional for both entities.

These many-to-many relationships are likely to be decomposed into one-to-many relationships. The mandatory/optional nature of the relationship must be preserved when this happens.

Weak and strong entities

An entity set that does not have a primary key is referred to as a weak entity set. The existence of a weak entity set depends on the existence of a strong entity set, called the identifying entity set. Its existence, therefore, is dependent on the identifying entity set.

The relationship must be many-to-one from weak to identifying entity. Participation of the weak entity set in the relationship must be mandatory. The discriminator (or partial key) of a weak entity set distinguishes weak entities that depend on the same specific strong entity. The primary key of a weak entity is the primary key of the identifying entity set + the partial key of the weak entity set.

Example: Many payments are made on a loan

• Payments don't exist without a loan.

• Multiple loans will each have a first, second payment and so on. So, each payment is only unique in the context of the loan which it is paying off.

The weak entity is commonly represented by two boxes.

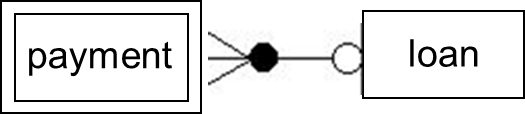
The payment is a weak entity; its existence is dependent on the loan entity.

Problems with entity-relationship (ER) models

In this section we examine problems that may arise when creating an ER model. These problems are referred to as connection traps, and normally occur due to a misinterpretation of the meaning of certain relationships. We examine two main types of connection traps, called fan traps and chasm traps, and illustrate how to identify and resolve such problems in ER models.

Fan traps

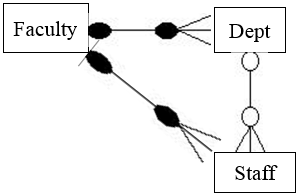
These occur when a model represents a relationship between entity types, but the pathway between certain entity occurrences is ambiguous. Look at the model below.

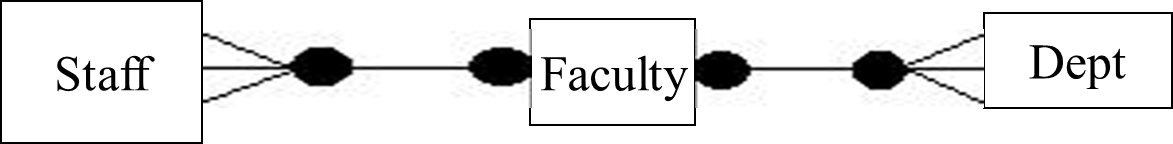
The above model looks okay at first glance, but it has a pitfall. The model says a faculty has many departments and many staff. Although the model seems to capture all the necessary information, it is difficult to know which department staff are affiliated to. To find out the departments the staff belong to, we will start from the staff entity. Through the relationship between staff and faculty, we are able to easily identify the faculties staff belong to. From the faculty, it's difficult to know the exact department because one faculty is associated with many departments.

The model below removes the fan trap from the model.

Chasm traps

These occur when a model suggests the existence of a relationship between entity types, but the pathway does not exist between certain entity occurrences.

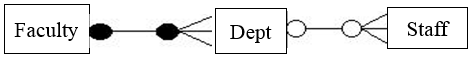
The model represents the facts that a faculty has many departments and each department may have zero or many staff. We can clearly note that, not all departments have staff and not all staff belong to a department. Examples of such staff in a university can include the secretary of the dean. He/she does not belong to any department.

It's difficult to answer the question, "Which faculty does the dean's secretary belong to?", as the secretary to the dean does not belong to any department.

We remove the 'chasm trap' by adding an extra relationship from staff to faculty.

Converting entity relationships into relations

When we have identified the main entities and the relationships that exist between them, we are in a position to translate the entity-relationship model we have created from a diagram into tables of data that will form the relations for our database. The nature of the relationships between entities will make a difference to the nature of the relations we construct; the cardinality, degree and membership class will all affect the structure of the database.

If we design a database by using an entity-relationship model, we need to be able to convert our design from a diagrammatic format into a series of relations that will hold the values of the actual data items.

It would be possible to create a number of relations so that each represented either an entity or relationship. This approach would generate a relational database that represented the entities and the relationships between them as identified in our data model, but it would suffer from a number of disadvantages. One disadvantage would be that the number of relations created could result in the database being unnecessarily large. There are also a number of insertion, update and deletion anomalies, which will be examined in the chapter on Normalisation, to which a database created in such a way would be vulnerable. To avoid these problems, we need to specify a method that allows us to create only those relations that are strictly necessary to represent our data model as a database. The way we do this is guided by the nature of the relationships between the entities, in terms of the cardinality and the membership class (participation condition).

Converting one-to-one relationships into relations

We can transform entity-relationship diagrams into relations by following simple rules which will specify the number of relations needed, depending on the cardinality (one-to-one, one-to-many or many-to-many) and the membership class (mandatory or optional) of the entities participating in the relationship. In the case of one-to-one relationships, the creation of one or two relations is sufficient, depending on whether participation is mandatory or optional.

Mandatory for both entities

A single relation will be able to represent the information represented by each entity and the relationship that exists between them.

If we consider an earlier example, with a one-to-one mandatory relationship between performers and agents, this could now be converted from a diagram into a relation as part of our database.

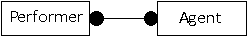
This part of an entity-relationship model can be converted into a single relation, Performer-details. This relation holds information about all the performers and their agents. The agents do not need to be held in a separate relation as each performer has one agent, and each agent represents only one performer.

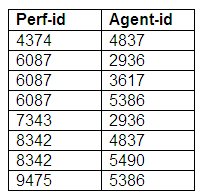
Relation: Performer-details

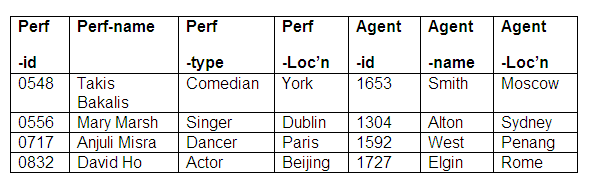
In the relation Performer-details above, we can see that all performer information is stored and can be accessed by the performer-id attribute, and all agent information can be extracted by means of the agent-id attribute.

As the relationship is one-to-one and mandatory in both directions, we do not need to store the performers and agents in separate relations, although we could choose to do so. (If we stored performers and agents in separate relations, we would then need to use the identifying attributes of performer-id and agent-id as foreign keys. This means that we would be able to identify the relevant agent in the Performer relation, and identify the appropriate performer in the Agent relation.)

Mandatory for one entity, optional for the other entity

In this case, two relations will be needed, one for each entity. The relationship could be mandatory for the first entity and optional for the second, or the other way around. There are therefore two possibilities for performers and agents.

In this first example, a performer must be represented by an agent, but an agent does not have to represent a performer. The relationship is therefore mandatory for a performer, but optional for an agent.

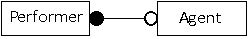
This would convert into two relations, one for each entity. The agent identifier is stored in the Performer relation in order to show the connection between agents and performers where appropriate. This is known as posting an identifier (or posting an attribute). It is important that the value of a posted identifier is not null.

Relation: Performer

Note that the agent identifier, agent-id, is held in the Performer relation. The attribute agent-id is a foreign key in the Performer relation. This means that we can identify which agent represents a particular performer.

We would not want to store the performer-id in the Agent relation for this example, as there are agents who do not represent performers, and there would therefore be a null value for the performer-id attribute in the Agent relation. We can see that there are agents in the Agent relation who do not represent performers, but all performers are represented by only one agent.

Relation: Agent

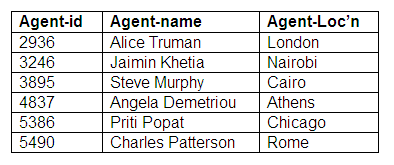
In the second example, an agent must represent a performer, but a performer does not need to have an agent. Here, the relationship is optional for a performer, but mandatory for an agent.

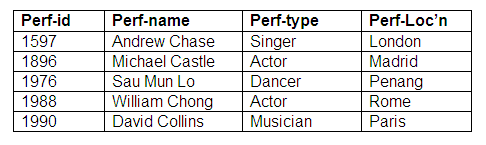
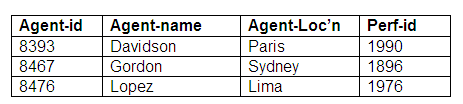
Again, this would translate into two relations, one for each entity. On this occasion, however, the link between performers and agents will be represented in the Agent relation rather than the Performer relation. This is because every agent will be associated with a performer, but not all performers will be linked to agents. The performer-id is a foreign key in the Agent relation. We cannot have the agent identifiers in the Performer relation as in some instances there will be no agent for a performer, and a null value for an agent identifier is not allowed, as it would contravene the rules on entity integrity.

Relation: Performer

Relation: Agent

Optional for both entities

In this scenario, a performer might or might not have an agent. Similarly, an agent might or might not represent a performer. However, if a performer does have an agent, that agent will not represent any other performers. The relationship between the two entities is one-to-one, but optional on both sides. In order to convert this relationship into a relational format, three relations will be needed, one for each entity and one for the relationship.

This means that it is possible to have a performer without an agent, and it is also permissible for an agent to have no performers. All performer details will be stored in the Performers relation, and all agent data will be held in the Agent relation. Where there is a performer with an agent, this will be shown in the relation Works-with, which will represent the relationship between the two entities.

Relation: Performer

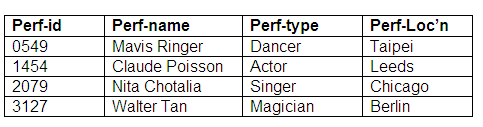
The relation Performers holds details of all the performers relevant to the database.

Relation: Agents

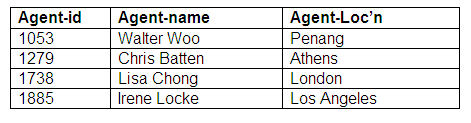
All agents within the database are stored in the relation Agents.

Relation: Works-with

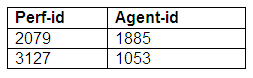
Note that the relation Works-with only has entries for those agents and performers who are linked together.

Converting one-to-many relationships into relations

Mandatory for both entities

If we consider the situation where a performer has a single agent, but each agent may represent a number of performers, and the relationship is mandatory for both entities, we have an entity-relationship as shown below.

If we convert this part of our data model into tables of data, we will have two relations (one for each entity). In order to maintain the relationship that exists between the two entities, we will hold a copy of the primary key of the entity at the "one" end of the relationship as one of the attributes associated with the entity at the "many" end of the relationship. In this example, the attribute agent-id is a foreign key in the relation Performers.

Relation: Performers

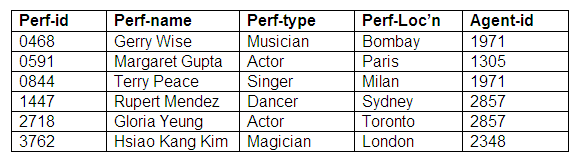
Relation: Agents

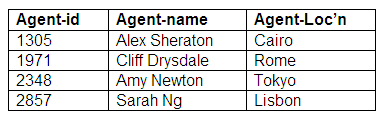
Mandatory for one entity, optional for another entity: many end mandatory

In this example, all performers must be represented by agents, and each performer has only one agent. The agents themselves need not be responsible for making bookings for performers, and can be involved in other activities.

The mandatory nature of the relationship for the performer is shown by the solid circle; the hollow circle indicates an optional relationship for an agent. This means that there must be a relation to represent performers, and another relation to represent agents. The links between performers and agents are shown by having the agent identifier stored against the appropriate performer in the Performer relation. The attribute agent-id is therefore a foreign key in the Performer relation. All performers must have an agent associated with them, but not all agents will be involved in a booking for a performer.

Relation: Performers

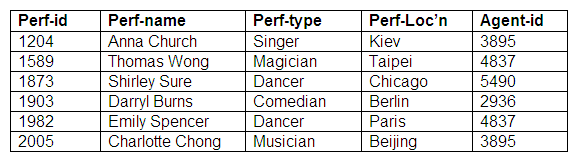
Relation: Agents

Mandatory for one entity, optional for another entity: many end optional

Here, agents may make bookings for performers, and performers may also make bookings for themselves. It is only possible for agents to make bookings for functions that involve performers. An agent may be responsible for making bookings for more than one performer. If a performer is represented by an agent, each performer may have only one agent.

The mandatory nature of the relationship for the agent is shown by the solid circle; the hollow circle indicates an optional relationship for a performer. This means that there must be a relation to represent performers, another relation to represent agents, and a third relation to represent those occasions when performers have booked through agents. The links between performers and agents are shown by having the agent identifier stored against the appropriate performer in the third relation.

Relation: Performers

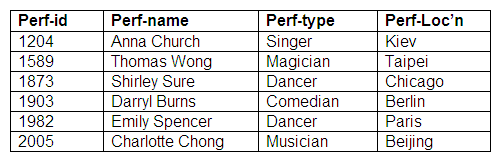
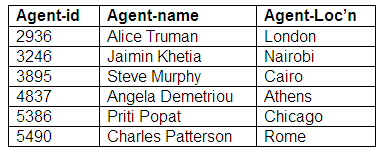
Relation: Agents

Relation: Agent-Performer

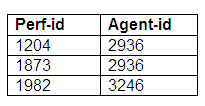
Optional for both entities

Here, agents may make bookings for performers, and performers may also make bookings for themselves. It is also possible for agents to make bookings for other functions that do not involve performers. An agent may be responsible for making bookings for a number of performers. If a performer is represented by an agent, each performer may have only one agent. The relationship is optional for both entities.

This relationship can be converted into three relations. There will be one relationship to represent the performers, another for the agents, and a third will store details of the relationship between performers and agents (where such a relationship exists).

Relation: Performers

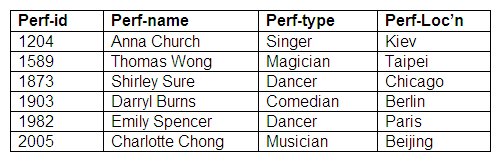
Relation: Agents

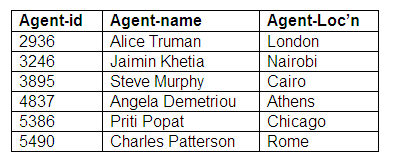
Relation: Agent-Performer

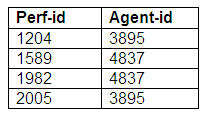
We can see from these relations that a performer may be represented by an agent, and an agent may represent more than one performer. Some performers do not have agents, and some agents do not represent performers.

Converting many-to-many relationships into relations

We know that if we are dealing with many-to-many relationships, we have to decompose them into two one-to-many relationships. Here we can see that if we leave a many-to-many relationship as it is, it will be represented by three relations just as if we had converted it into two one-to-many relationships.

Mandatory for both entities

In this example, all performers must be represented by agents, and all agents must represent performers. It is not possible for performers to represent themselves when making bookings, neither is it possible for agents to make bookings that do not involve performers. (Note that this does not imply that each performer has one agent, and each agent represents one performer; that would imply a one-to-one relationship).

Three relations are required to represent a relationship of this kind between two entities, one for each entity and one for the relationship itself, i.e. one to represent the performers, another to represent the agents, and a third to represent the relationship between the performers and the agents.

Relation: Performers

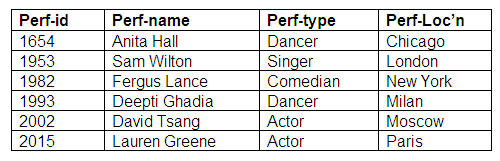
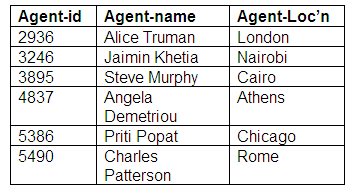
Relation: Agents

Relation: Agent-Performers

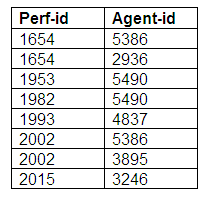
The Agent-Performers relation shows us that all performers are represented by agents, and that all agents represent performers. Some performers are represented by more than agent, and some agents represent more than one performer. We now have three relations representing the many-to-many relationship mandatory for both entities.

Mandatory for one entity, optional for the other entity

The first possibility is that the performer entity is mandatory, but the agent entity is optional. This would mean that performers cannot make bookings for themselves, but depend on a number of agents to make bookings for them. The relationship is mandatory for the performer. An agent, however, is allowed to make bookings for a number of performers, and may also agree bookings for events that do not involve performers, such as exhibitions or conferences. The relationship is optional for the agent.

The entity relationship diagram above shows that it is mandatory for performers, but optional for agents to participate. This is translated into three relations below. Note that in the relation Agent-Performers, all performers are represented by an agent (or more than one agent). There are some agents in the Agent relation who do not appear in Agent-Performers because they do not represent performers.

Relation: Performers

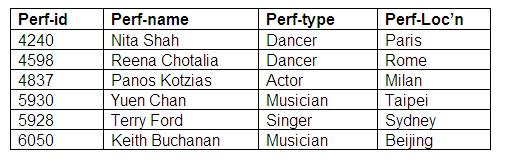
Relation: Agents

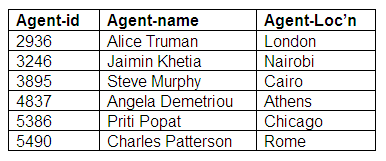
Relation: Agent-Performers

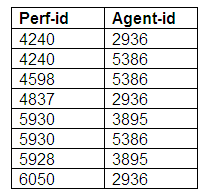
The second possibility for this kind of relationship is that the performer entity is optional but the agent entity is mandatory. In this case, a performer might have one or more agents, but an agent must represent several performers. Here, a performer could make a booking personally, or could have a booking made by a number of different agents. The agents can only make bookings for performers, and for no other kind of event.

The entity relationship diagram above illustrates optional participation for a performer, but mandatory participation by an agent.

Relation: Performers

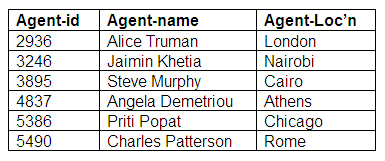
Relation: Agents

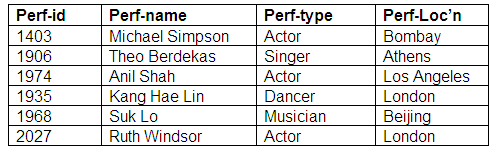
Relation: Agent-Performers

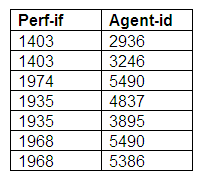
The relation Agent-Performers shows that all agents represent one or more performers. Some performers are represented by more than one agent, whereas other performers are not represented by agents at all.

Optional for both entities

We could imagine a situation where each performer could be represented by a number of different agents, and could also make bookings without using an agent. In addition, each agent could act for a number of different performers, and the agents could also make bookings that did not involve performers. This would be modelled by a many-to-many relationship between performers and agents that was optional for both entities.

In order to represent this relationship between two entities, we would need three relations, one for each entity and one for the relationship itself. The reason we need three relations rather than just two (one for each entity) is that the relationship is optional. This means that if we were to store the identifier of one entity in the relation of the other, there would be times when we would have a null value for the identifier as no relationship exists for a particular instance of the entity. We cannot have a null value for an identifier, and therefore we show the relationships that do exist explicitly in a third relation.

Relation: Performers

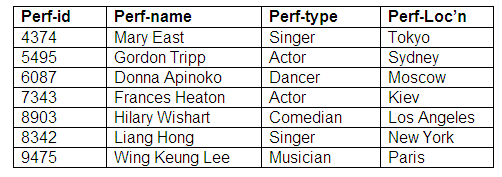
Relation: Agents

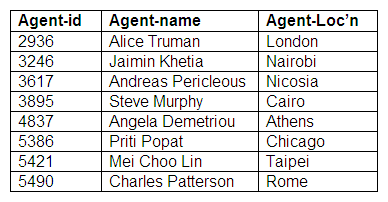
Relation: Agent-Performers

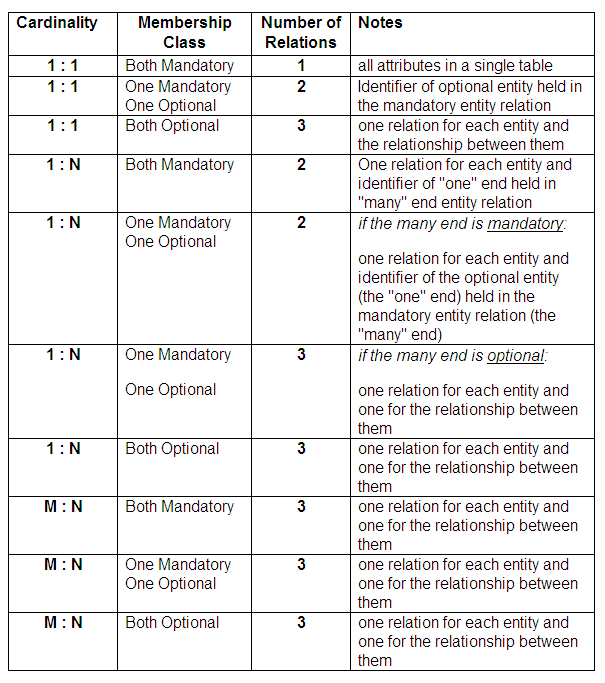
Summary of conversion rules

The following table provides a summary of the guidelines for converting components of an entity-relationship diagram into relations. We need to be certain that if we store an identifier for one entity in a relation representing another entity, that the identifier never has a null value. If we have a null value for an identifier, we will never be able to find the other details that should be associated with it.

Review questions

• Case study: Theatrical database

Consider the design of a database in the context of the theatre. From the description given below, identify the entities and the relationships that exist between them. Use this information to create an entity-relationship diagram, with optional and mandatory membership classes marked. How many entities have you found? Now translate this data model into relations (tables of data). Don't forget the guidelines in order to decide how many relations you will need to represent entities and the relationships between them. You should also think about areas where you don't have enough information, and how you would deal with this kind of problem. You might also find that there is information that you don't need for building the data model.

"Authors are responsible for writing plays that are performed in theatres. Every time a play is performed, the author will be paid a royalty (a sum of money for each performance).

Plays are performed in a number of theatres; each theatre has maximum auditorium size, and many people attend each performance of a play. Many of the theatres have afternoon and evening performances.

Actors are booked to perform roles in the plays; agents make these bookings and take a percentage of the fee paid to the actor as commission. The roles in the plays can be classified as leading or minor roles, speaking or non-speaking, and male or female."

• Explain the difference between entities and attributes. Give examples of each.

• Distinguish between the terms 'entity type' and 'entity instance', giving examples.

• Distinguish between the terms 'primary key' and 'candidate key', giving examples.

• Explain what is meant by one-to-one, one-to-many and many-to-many relationships between entities, giving an example of each.

• How are many-to-many relationships implemented in Relational databases?

Source: https://www.cs.uct.ac.za/mit_notes/database/htmls/chp06.html

Posted by: mandikibele0194367.blogspot.com